Imagine que você tem $10 em sua conta bancária e o banco promete que a quantia aumentará 6% ao ano. Em 12 anos, a soma dobrará e chegará a $ 20; em 24 anos, será de $ 40. Isso é juros compostos em ação. O melhor é que, quanto mais longo for o seu composto de poupança, mais rápido ele cresce.
Então, qual é a definição de juros compostos? É um aumento constante do capital de investimento em detrimento do lucro, enquanto a receita recebida é envolvida na obtenção de novo capital para o próximo período de faturamento. A vantagem dos juros compostos reside no crescimento acelerado da poupança, devido ao constante reinvestimento. Nos bancos, isso também é chamado de capitalização.
Gere lucro em 1 minuto
Como funcionam os juros compostos?
O criador da teoria da relatividade, Albert Einstein, disse certa vez sobre os juros compostos: “Os juros compostos são a oitava maravilha do mundo. Aqueles que entendem, ganham e aqueles que não entendem, vão pagar por isso.”
Antes de entendermos como calcular os juros compostos de um investimento, vamos entender os juros simples. Eles são frequentemente usados para calcular o lucro em um depósito bancário, com a retirada de receita durante os períodos de liquidação. Por exemplo, se uma quantia de $100 for investida a uma taxa de juros de 10% ao ano, em um ano ela se transformará em $ 110—e em 10 anos, o valor inicial terá dobrado.
1º ano: $ 100 + $ 100*0,10 = $ 110
1º ano: $ 110 + $ 100*0,10 = $ 120
Ano 10: $ 100 + $ 100*0,10*10 anos = $ 200
E agora, usando o mesmo exemplo, vamos ver como funcionam os juros compostos com a capitalização anual.
1º ano: 100 + 10% = $ 110
2º ano: 110 + 10% = $ 121
10º ano: 236 + 10% = $ 259
Estratégias eficazes em sua caixa de entrada
Inscreva-se e descubra uma fonte de conhecimentos sobre trading
Ótimo! Confira seu e-mail
Enviamos um e-mail para você confirmar a assinatura
Houve um erro
Recarregue a página. Se não resolver, tente de novo depois
Calculadora e fórmula de juros compostos
O valor do lucro no exemplo acima pode ser ainda maior se você aplicar a capitalização mensal ao invés da anual. Em nosso exemplo, o total após 10 anos seria de $ 271. Para simplificar os cálculos, considere uma calculadora de juros compostos on-line. Pode ser também uma calculadora mensal de juros compostos.
Se você mesmo deseja calcular o crescimento composto, considere a seguinte fórmula:
C=C0*(1+s/100)*n
Onde:
C é o valor total
C0 – o valor do depósito inicial
s – retorno anual em %
n é o número de períodos de investimento
Ao calcular juros compostos com capitalização, lembre-se de que não apenas o valor inicial do depósito, mas também cada acúmulo de lucro traz receita. Ao mesmo tempo, o valor aumenta em alta velocidade e, quanto mais frequentemente o lucro for fixado, maior será a receita.
A vantagem dos juros compostos sobre os juros simples é ainda mais convincente no gráfico. Suponha que o depósito inicial de um investidor seja $ 100 com um rendimento de 8% ao ano sem reinvestimento. Nesse caso, em 30 anos, o capital resultante será igual a $ 340. O mesmo período com juros compostos resultará em $ 1.006.
11 citações que podem mudar sua negociação
Confira estas poderosas pepitas de sabedoria de traders, economistas e empresários famosos.
Ler mais
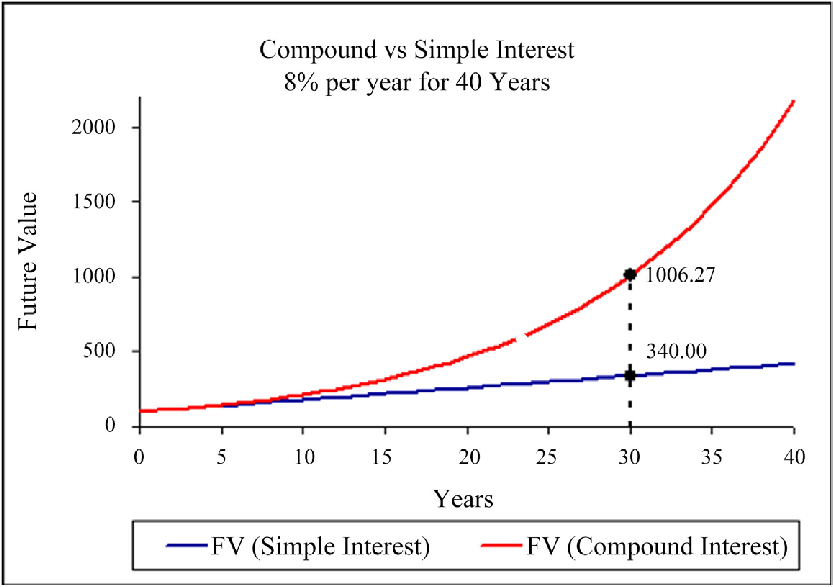
Os juros compostos garantem maior economia?
Como você pode ver, os juros compostos se manifestam apenas com investimentos de longo prazo. É por isso que é mais adequado para investidores jovens e pacientes. Infelizmente, essa combinação é rara: a ambição dos jovens e sua propensão a correr riscos muitas vezes levam ao fracasso.
Por outro lado, no longo prazo, o papel da inflação torna-se vívido. Portanto, seria mais correto ajustar seu valor pela inflação, o que dará números completamente diferentes.
Einstein é frequentemente creditado com a descoberta da “Regra 72”. Este é um método aproximado de determinar quanto tempo levará para um investimento dobrar a uma taxa de juros anual fixa. Basta dividir 72 pela taxa de retorno anual. Por exemplo, com um rendimento de 12%, você ganha 6 anos. Esta regra só pode funcionar no setor bancário e no mercado de títulos. Para retornos anuais baixos, acaba sendo quase preciso. À medida que a lucratividade aumenta, sua precisão diminui. Isso é especialmente verdadeiro no mercado de ações, com suas enormes flutuações entre lucros e perdas.
Fontes:
What is compound interest?, Investor.gov
The Power of Compound Interest: Calculations and Examples, Investopedia
Negociação com até 90% de lucro
<span>Curtir</span>
4 min 
