Imagine you have $10 in your bank account, and the bank promises the sum will increase by 6 percent annually. In 12 years, the sum will double and reach $20; in 24 years, it’ll be at $40. That’s compound interest in action. The best thing is that the longer your savings compound, the faster they grow.
So what is the compound interest definition? It is a constant increase in investment capital at the expense of profit, while the income received is involved in obtaining new capital for the next billing period. The advantage of compound interest lies in the accelerated growth of savings, due to constant reinvestment. In banks, this is also called capitalization.
Start from $10, earn to $1000
How does compound interest work?
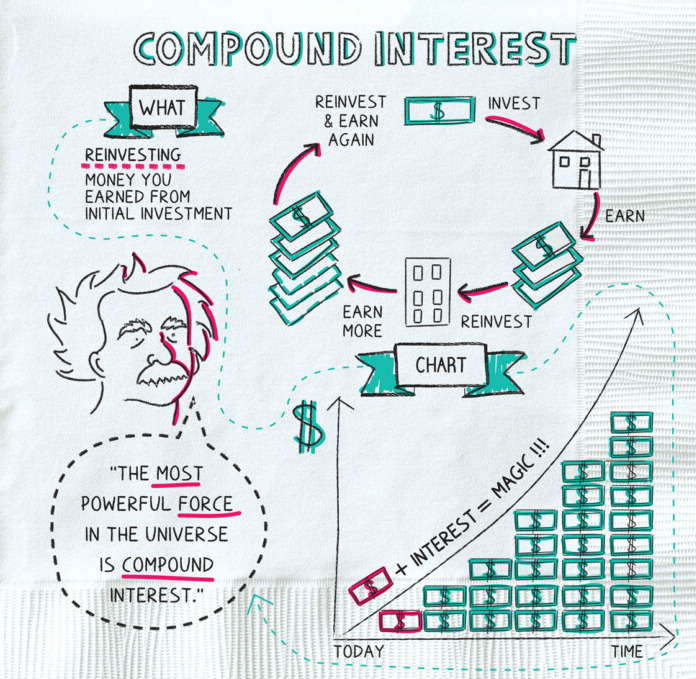
The creator of the theory of relativity, Albert Einstein, once said this about compound interest: “Compound interest is the eighth wonder of the world. Those who understand it, earn it and those who don’t, will pay for it.”
Before we understand how to calculate compound interest on an investment, let’s understand simple interest. It is often used when calculating profit on a bank deposit, with the withdrawal of income during settlement periods. For example, if an amount of $100 is invested at a 10% interest rate per annum, then in a year it will turn into $110—and in 10 years, the initial amount will have been doubled.
1st year: $100 + $100*0.10 = $110
1st year: $110 + $100*0.10 = $120
Year 10: $100 + $100*0.10*10 years = $200
And now, using the same example, let’s see how compound interest works with annual capitalization.
1st year: 100 + 10% = $110
2nd year: 110 + 10% = $121
10th year: 236 + 10% = $259
Effective strategies in your mailbox
Subscribe and discover a fund of trading knowledge
Great! Please check your email
We’ve sent you an email to confirm your subscription
Something went wrong
Try reloading the page. If that doesn’t help, please try again later
Compound interest calculator and formula
The profit value in the example above can be even greater if you apply monthly capitalization rather than annual. In our example, the total after 10 years would be $271. To simplify calculations, consider an online compound interest calculator. It can also be a monthly compound interest calculator.
If you wish to calculate the compound growth yourself, consider the following formula:
C=C0*(1+s/100)*n
Where:
C is the total amount,
C0 – the amount of the initial deposit,
s – annual return in %,
n is the number of investment periods.
When calculating compound interest with capitalization, keep in mind that not only the initial amount of the deposit but also each accrual of profit brings income. At the same time, the amount increases at a high speed, and the more often profit is fixed, the higher the income will be.
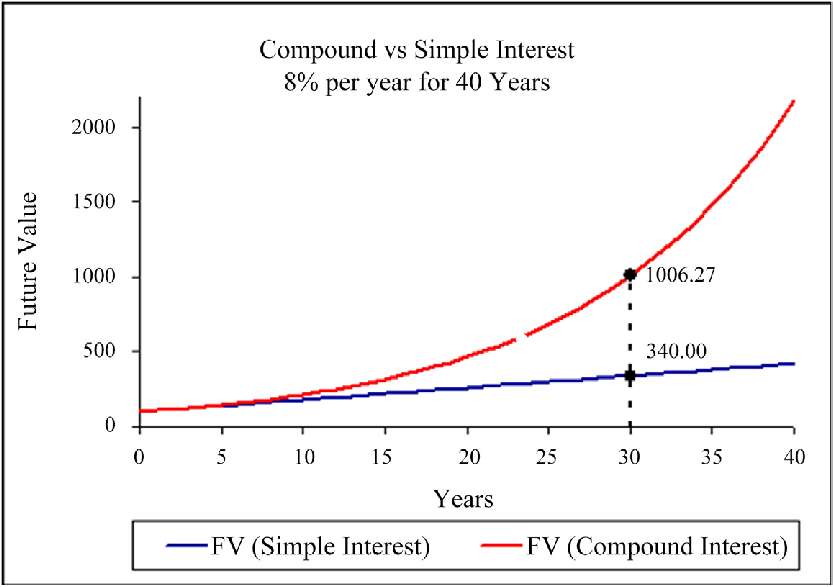
The advantage of compound interest over simple interest is even more convincing on the chart. Suppose an investor’s initial deposit is $100 with a yield of 8% per annum without reinvestment. In this case, in 30 years, the resulting capital will be equal to $340. The same period with compound interest will result in $1006.
Does compound interest guarantee increased savings?
As you can see, compound interest manifests itself only with long-term investment. That is why it is more suitable for young, patient investors. Unfortunately, this combination is rare: the ambition of young people and their propensity to take risks often leads to failures.
On the other hand, in the long term, the role of inflation becomes vivid. Therefore, it would be more correct to adjust its value for inflation, which will give completely different numbers.
Einstein is often credited with the discovery of “Rule 72.” This is a rough method of determining how long it will take for an investment to double at a fixed annual interest rate. It is enough to divide 72 by the annual rate of return. For example, with a yield of 12%, you get 6 years. This rule can only work in the banking sector and the bond market. For low annual returns, it turns out to be almost accurate. As profitability increases, its accuracy decreases. This is especially true of the stock market with its huge fluctuations between profits and losses.
Sources:
What is compound interest?, Investor.gov
The Power of Compound Interest: Calculations and Examples, Investopedia
Trading with up to 90% profit
+2 <span>Like</span>
4 min 
